SGU 112:a^b-b^a
题目链接:http://acm.sgu.ru/problem.php?contest=0&problem=112
题目大意:
输入a,b输出a^b-b^a的值。(1<=a,b<=100)
解题思路:
肯定是用高精度算法,可是比较懒阿,先用JAVA写一个,然后C++的以后写吧。
解题代码:
import java.math.*;
import java.io.*;
import java.util.*;
public class Solution{
public static void main(String[] args){
Scanner cin=new Scanner(System.in);
int a,b;
while(cin.hasNext()){
a=cin.nextInt();
b=cin.nextInt();
System.out.println(BigInteger.valueOf(a).pow(b).subtract(BigInteger.valueOf(b).pow(a)));
}
}
}
扩展知识:http://blog.csdn.net/soberman/archive/2009/03/10/3978074.aspx
SGU 113: Nearly prime numbers
题目链接:http://acm.sgu.ru/problem.php?contest=0&problem=113
题目大意:
如果一个数可以分解成2个素数的乘积,那么就输出yes否则输出no.
解题思路:
先筛选出素数,然后判断找到那个能整除这个数的素数,判断商是否为素数就行啦!起先题目给看错了以为是相邻的素数的积。
解题代码:
#include<iostream>
#include<cmath>
#include<cstring>
using namespace std;
#define Max 50000
bool isprime[Max];
int prime[Max];
int cp;
void mkprime(){
cp=1;
memset(isprime,true,Max);
prime[0]=2;
for(int i=2;i<Max;i++){
if(isprime[i]==true){
prime[cp++]=i;
for(int j=1;i*j<Max;j++)
isprime[i*j]=false;
}
}
}
bool isp(int n){
if(n==1) return false;
if(((n!=2)&&!(n%2))||((n!=3)&&!(n%3))||
((n!=5)&&!(n%5))||((n!=7)&&!(n%7)))
return false;
int t=sqrt(n);
for(int i=2;i<t;i++)
if(n%i==0)
return false;
return true;
}
int main(){
mkprime();
int cas;
cin>>cas;
while(cas--){
int n;
cin>>n;
int flag=0;
for(int i=0;i<cp;i++){
if(n%prime[i]==0)
if(isp(n/prime[i])){
flag=1;
break;
}
}
if(flag)
cout<<"Yes"<<endl;
else
cout<<"No"<<endl;
}
return 0;
}
SGU 102: Coprimes
题目链接:http://acm.sgu.ru/problem.php?contest=0&problem=102
题目大意:
求不大于N且与N互质的数的个数。
解题思路:
刚开始就想到暴力法,枚举每个数看看是不是gcd(n,i)==1。
后来想到了欧拉函数,这不就是典型的欧拉函数题,先分解素数然后求欧拉函数。
欧拉函数法用的时间是暴力法的一半。
解题代码:
#include<iostream>
using namespace std;
int gcd(int a,int b){
return b?gcd(b,a%b):a;
}
int main(){
int n;
while(cin>>n){
int sum=0;
for(int i=1;i<=n;i++){
if(gcd(n,i)==1)
sum++;
}
cout<<sum<<endl;
}
}
#include<iostream>
#include<cstring>
using namespace std;
#define Max 10000
bool isprime[Max+10];
int prime[Max+10];
int countp;
void mkprime(int n){
countp=1;
memset(isprime,true,Max+10);
prime[0]=2;
for(int i=3;i<=n;i+=2){
if(isprime[i]==true){
prime[countp++]=i;
for(int j=1;i*j<=n;j++)
isprime[i*j]=false;
}
}
}
int eular(int n){
for(int i=0;prime[i]<=n&&i<countp;i++)
if(n%prime[i]==0){
n/=prime[i];
n*=prime[i]-1;
}
return n;
}
int main(){
int n;
while(cin>>n){
mkprime(n);
if(n==1)
cout<<1<<endl;
else
cout<<eular(n)<<endl;
}
}
扩展知识:
UVA 369: Combinations
题目大意:
GIVEN:
![]()
Compute the EXACT value of:
![]()
给你N和M求C。
解题思路:
由于直接求出阶乘数据庞大,要用高精度算法。但是据题目说答案不超过32位,所以就用新的方法来做。把公式转化为
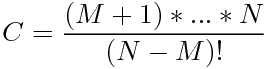
然后把m+1到n都存入数组,用(n-m)到1去和数组的数一起除以它们的最大公约数。最后把数组里面的数相乘起来就是答案。
解题代码:
#include<iostream>
using namespace std;
typedef long long ll;
ll s[105];
ll gcd(ll a,ll b){
return a%b==0?b:gcd(b,a%b);
}
int main(){
ll n,m;
while(cin>>n>>m&&m+n){
for(int i=1;i<=n;i++)
s[i]=i;
ll t=n-m,sum=1;
if(t!=0){
while(t!=1){
for(int i=m+1,j=t;i<=n&&j!=1;i++){
ll g=gcd(s[i],j);
s[i]/=g;
j/=g;
}
t--;
}
for(int i=m+1;i<=n;i++)
sum*=s[i];
}
cout<<n<<" things taken "<<m<<" at a time is "<<sum<<" exactly."<<endl;
}
return 0;
}
UVA 575: Skew Binary
题目大意:
定义一个新的进制数,把这种新数转化为十进制数。
解题代码:
#include<iostream>
using namespace std;
int main(){
string s;
while(cin>>s&&s!="0"){
int sum=0;
int len=s.length();
for(int i=0;i<len;i++)
sum+=(s[i]-'0')*((1<<(len-i))-1);
cout<<sum<<endl;
}
}