SGU 135: Drawing Lines
题目链接:http://acm.sgu.ru/problem.php?contest=0&problem=135
题目大意:
n条直线能把平面分成最多几个空间。
解题思路:
可以推出f(n)=f(n-1)+n;然后扩展得到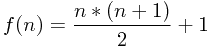 .
.
解题代码:
#include<iostream>
using namespace std;
int main(){
long long n;
cin>>n;
cout<<(n*(n+1)/2+1)<<endl;
return 0;
}
扩展知识:http://mathworld.wolfram.com/CircleDivisionbyLines.html
SGU 115: Calendar
题目链接:http://acm.sgu.ru/problem.php?contest=0&problem=115
题目大意:
输出2001年的某天的星期几。
解题思路:
只要注意2001年的二月是28天,还要判断日期是否合法。
解题代码:
#include<iostream>
using namespace std;
bool ok(int n,int m){
if(m<=0||m>12) return false;
if((m==1)||(m==3)||(m==5)||(m==7)||(m==8)||(m==10)||(m==12))
if(n<=0||n>31) return false;
if((m==4)||(m==6)||(m==9)||(m==11))
if(n<=0||n>30) return false;
if(m==2)
if(n<=0||n>28) return false;
return true;
}
int day(int n,int m){
return n+31*((m>1)+(m>3)+(m>5)+(m>7)+(m>8)+(m>10)) \
+30*((m>4)+(m>6)+(m>9)+(m>11))+28*(m>2);
}
int main(){
int n,m;
while(cin>>n>>m){
if(ok(n,m)){
int w=day(n,m)%7;
if(w) cout<<w<<endl;
else cout<<7<<endl;
}
else
cout<<"Impossible"<<endl;
}
return 0;
}
SGU 123: The sum
题目链接:http://acm.sgu.ru/problem.php?contest=0&problem=123
题目大意:
求斐波那契数前n个的和。
解题思路:
一个数组存斐波那契数,一个数组存前n个的和。
解题代码:
#include<iostream>
using namespace std;
long long f[42]={1,1};
long long s[42]={1,2};
int main(){
for(int i=2;i<42;i++){
f[i]=f[i-1]+f[i-2];
s[i]=s[i-1]+f[i];
}
int n;
while(cin>>n)
cout<<s[n-1]<<endl;
return 0;
}
SGU 105: Div 3
题目链接:http://acm.sgu.ru/problem.php?contest=0&problem=105
题目大意:
有一个数列1,12,123,1234,...,12345678910,1234567891011,...,求第N个数前有几个数能被3整除包括N.
解题思路:
能被3整除的数的特点是各个位上的和加起来能被3整除,看规律可知每3个数中有一个数不能被3整除,那个数就是序数跟3取模是1的那个数。
解题代码:
#include<iostream>
#include<stdio.h>
using namespace std;
int main(){
long long n,t,m;
while(cin>>n){
m=n/3*2;
if(n%3!=0){
t=n%3-1;
m+=t;
}
cout<<m<<endl;
}
return 0;
}
SGU 102: Coprimes
题目链接:http://acm.sgu.ru/problem.php?contest=0&problem=102
题目大意:
求不大于N且与N互质的数的个数。
解题思路:
刚开始就想到暴力法,枚举每个数看看是不是gcd(n,i)==1。
后来想到了欧拉函数,这不就是典型的欧拉函数题,先分解素数然后求欧拉函数。
欧拉函数法用的时间是暴力法的一半。
解题代码:
#include<iostream>
using namespace std;
int gcd(int a,int b){
return b?gcd(b,a%b):a;
}
int main(){
int n;
while(cin>>n){
int sum=0;
for(int i=1;i<=n;i++){
if(gcd(n,i)==1)
sum++;
}
cout<<sum<<endl;
}
}
#include<iostream>
#include<cstring>
using namespace std;
#define Max 10000
bool isprime[Max+10];
int prime[Max+10];
int countp;
void mkprime(int n){
countp=1;
memset(isprime,true,Max+10);
prime[0]=2;
for(int i=3;i<=n;i+=2){
if(isprime[i]==true){
prime[countp++]=i;
for(int j=1;i*j<=n;j++)
isprime[i*j]=false;
}
}
}
int eular(int n){
for(int i=0;prime[i]<=n&&i<countp;i++)
if(n%prime[i]==0){
n/=prime[i];
n*=prime[i]-1;
}
return n;
}
int main(){
int n;
while(cin>>n){
mkprime(n);
if(n==1)
cout<<1<<endl;
else
cout<<eular(n)<<endl;
}
}
扩展知识:
SGU 介绍
SGU 是俄罗斯萨拉托夫国立大学(Saratov State University)用于培养ACM选手的训练网站。这个网站的建成时期较晚,但 随着比赛的举行以及新题目的加入,这个题库的题目也日渐丰富。这个题库的一大特点就是 Online Judge功能强大,它不仅使你避开了多数据处理的 繁琐操作,还能告诉你程序错在了第几个数据。这一 点虽然与ACM的Judge有些出入,但是却方便了调试程序。与UVA相比,这里的题目 在时间空间上 要求都比较严 格,而且更多的考察选手对算法的掌握情况,所以特别推荐冲击NOI的选手也来做一做。题目数量很少,但题题精炼,每做一道题都会让你的编程水平上升.在有一定编程水平之后可以试着做做,要争取做出每一道题.如果sgu能全部AC的话... 那这个人不是抄袭就是神牛...注意status需要通过左边的"status online"链接来看,而且sgu速度稍慢并且不太稳定.总之是非常特别以及及其应该推荐的OJ.
打算和UVA一起做,UVA最近经常崩溃,无奈只好在崩溃时候去SGU溜达下,发现SGU的题目确实是非常强大,肯定要做一下,跟UVA一样按照AC数大小来做!解题报告一样AC一题发一题。